Grafos

De aquí se podría deducir que un grafo es básicamente un objeto geométrico aunque en realidad sea un objeto combinatorio, es decir,un conjunto de puntos y un conjunto de líneas tomado de entre el conjunto de líneas que une cada par de vértices. Por otro lado, debido a su generalidad y a la gran diversidad de formas que pueden usarse, resulta complejo tratar con todas las ideas relacionadas con un grafo.
Para facilitar el estudio de este tipo de dato, a continuación se realizará un estudio de la teoría de grafos desde el punto de vista de las ciencias de la computación, considerando que dicha teoría es compleja y amplia,aquí sólo se realizará una introducción a la misma, describiéndose el grafo como un tipo de dato y mostrándose los problemas típicos y los algoritmos que permiten solucionarlos usando un ordenador.
Los grafos son estructuras de datos no lineales que tienen una naturaleza generalmente dinámica, u estudio podría dividirse en dos grandes bloques; grafos dirigidos y grafos no dirigidos (pueden ser considerados un caso particular de los anteriores).
Un ejemplo de grafo dirigido lo constituye la red de aguas de una ciudad ya que cada tubería sólo admite que el agua la recorra en un único sentido, por el contrario, la red de carreteras de un país representa en general un grafo no dirigido, puesto que una misma carretera puede ser recorrida en ambos sentidos. No obstante, podemos dar unas definiciones generales para ambos tipos.
A continuación daremos definiciones de los dos tipos de grafos y de los conceptos que llevan asociados.
Notación y conceptos
Un grafo G es un conjunto en el que hay definida una relación binaria,es decir, G=(V,A) tal que V es un conjunto de objetos a los que denominaremos vértices o nodos y
A Í V x V es una relación binaria a cuyos elementos denominaremos arcos o aristas.
Dados x, y Î V, puede ocurrir que:
Ø (x, y) Î A, en cuyo caso diremos que x e y están unidos mediante un arco y,
Ø (x, y) Ï A, en cuyo caso diremos que no lo están.
Si las aristas tienen asociada una dirección(las aristas (x,y) y (y,x) no son equivalentes) diremos que el grafo es dirigido,en otro caso ((x,y)=(y,x)) diremos que el grafo es no dirigido.

Veamos algunos conceptos sobre grafos:
· Diremos que un grafo es completo si A=VxV,o sea,si para cualquier pareja de vértices existe una arista que los une(en ambos sentidos si el grafo es no dirigido).El número de aristas será:
Para grafos dirigidos:
Para grafos no dirigidos:

donde n=|V| .
· Un grafo dirigido es simétrico si para toda arista (x, y) Î A también aparece la arista (y, x) Î A y es antisimétrico si dada una arista (x, y) Î A implica que (y, x) Ï A.
· Tanto a las aristas como a los vértices les puede ser asociada información, a esta información se le llama etiqueta, si la etiqueta que se asocia es un número se le llama peso,costo o longitud, un grafo cuyas aristas o vértices tienen pesos asociados recibe el nombre de grafo etiquetado o ponderado.
· El número de elementos de V se denomina orden del grafo, un grafo nulo es un grafo de orden cero.
· Se dice que un vértice x es incidente a un vértice y si existe un arco que vaya de x a y ((x, y) Î A),a x se le denomina origen del arco y a y extremo del mismo, de igual forma se dirá que y es adyacente a x, en el caso de que el grafo sea no dirigido si x es adyacente (resp. incidente) a y entonces y también es adyacente (resp. incidente) a x.
· Se dice que dos arcos son adyacentes cuando tienen un vértice común que es a la vez origen de uno y extremo del otro.
· Se denomina camino (algunos autores lo llaman cadena si se trata de un grafo no dirigido)en un grafo dirigido a una sucesión de arcos adyacentes:
C={(v1,v2),(v2,v3),...,(vn-1,vn), vi Î V}.
C={(v1,v2),(v2,v3),...,(vn-1,vn), vi Î V}.
· La longitud del camino es el número de arcos que comprende y en el caso en el que el grafo sea ponderado se calculará como la suma de los pesos de las aristas que lo constituyen.
· Un camino se dice simple cuando todos sus arcos son distintos y se dice elemental cuando no utiliza un mismo vértice dos veces.Por tanto todo camino elemental es simple y el recíproco no es cierto.
· Un camino se dice Euleriano si es simple y además contiene a todos los arcos del grafo.
· Un circuito (o ciclo para grafos no dirigidos) es un camino en el que coinciden los vértices inicial y final, un circuito se dice simple cuando todos los arcos que lo forman son distintos y se dice elemental cuando todos los vértices por los que pasa son distintos. La longitud de un circuito es el número de arcos que lo componen. Un bucle es un circuito de longitud 1 (están permitidos los arcos de la forma (i,i) y notemos que un grafo antisimétrico carecería de ellos).
· Un circuito elemental que incluye a todos los vértices de un grafo lo llamaremos circuito Hamiltoniano.
· Un grafo se denomina simple si no tiene bucles y no existe más que un camino para unir dos nodos.
· Diremos que un grafo no dirigido es bipartido si el conjunto de sus vértices puede ser dividido en dos subconjuntos (disjuntos) de tal forma que cualquiera de las aristas que componen el grafo tiene cada uno de sus extremos en un subconjunto distinto, un grafo no dirigido será bipartido si y sólo si no contiene ciclos con un número de aristas par.
· Dado un grafo G=(V,A),diremos que G'=(V,A' ) con A' Ì A es un grafo parcial de G y un subgrafo de G es todo grafo G'=(V',A') con V' Í V y A' Í A donde A' será el conjunto de todas aquellas aristas que unían en el grafo G dos vértices que están en V'., se podrían combinar ambas definiciones dando lugar a lo que llamaremos subgrafo parcial .

· Se denomina grado de entrada de un vértice x al número de arcos incidentes en él, se denota de (x).
· Se denomina grado de salida de un vértice x al número de arcos adyacentes a él, se denota ds (x).
· Para grafos no dirigidos tanto el grado de entrada como el de salida coinciden y hablamos entonces de grado y lo notamos por d (x).
· A todo grafo no dirigido se puede asociar un grafo denominado dual construido de la siguiente forma:
G (V, A) ------> G' (V', A' )
donde A' está construido de la siguiente forma: si e1,e2 Î a A son adyacentes --> (e1,e2) Î a A' con e1,e2 Î a V', en definitiva, para construir un grafo dual se cambian vértices por aristas y viceversa.

· Dado un grafo G, diremos que dos vértices están conectados si entre ambos existe un camino que los une.
· Llamaremos componente conexa a un conjunto de vértices de un grafo tal que entre cada par de vértices hay al menos un camino y si se añade algún otro vértice esta condición deja de verificarse. Matemáticamente se puede ver como que la conexión es una relación de equivalencia que descompone a V en clases de equivalencia,cada uno de los subgrafos a los que da lugar cada una de esas clases de equivalencia constituiría una componente conexa. Un grafo diremos que es conexo si sólo existe una componente conexa que coincide con todo el grafo.
( IMÁGENES )
foto
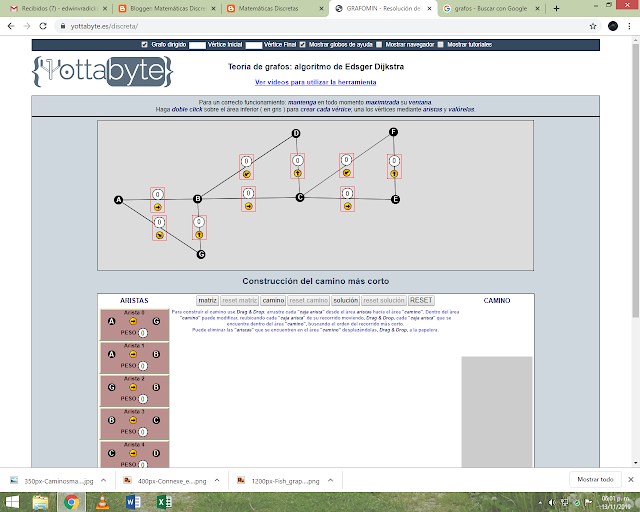
Capturas de pantalla
1 programa
2 programa








No hay comentarios.:
Publicar un comentario